Given the root of a binary search tree, and an integer k, return the kth smallest value (1-indexed) of all the values of the nodes in the tree.
풀이
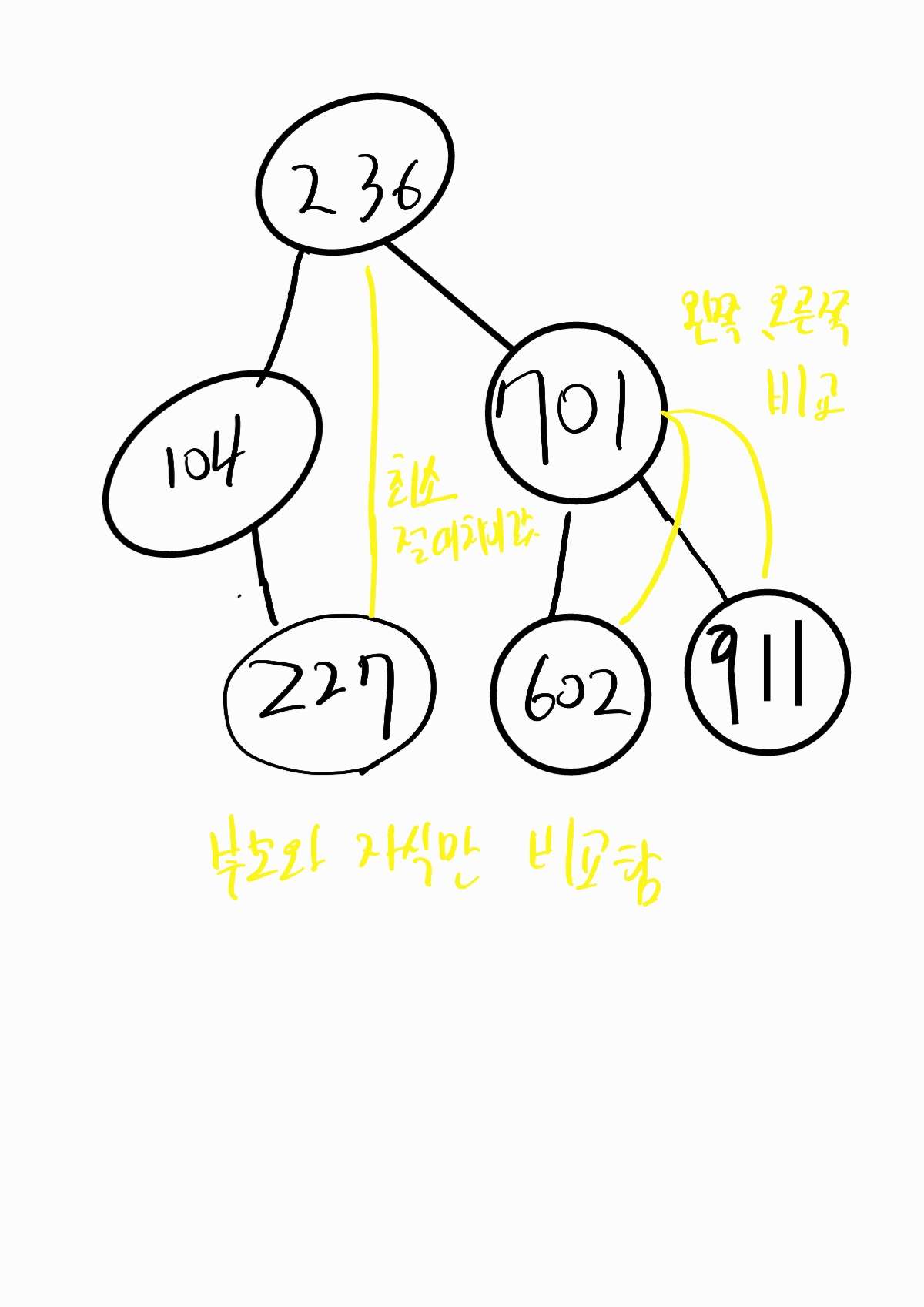
이진트리에서 k번째로 작은 숫자를 반환하는 문제이다. (인덱스 1 부터시작)
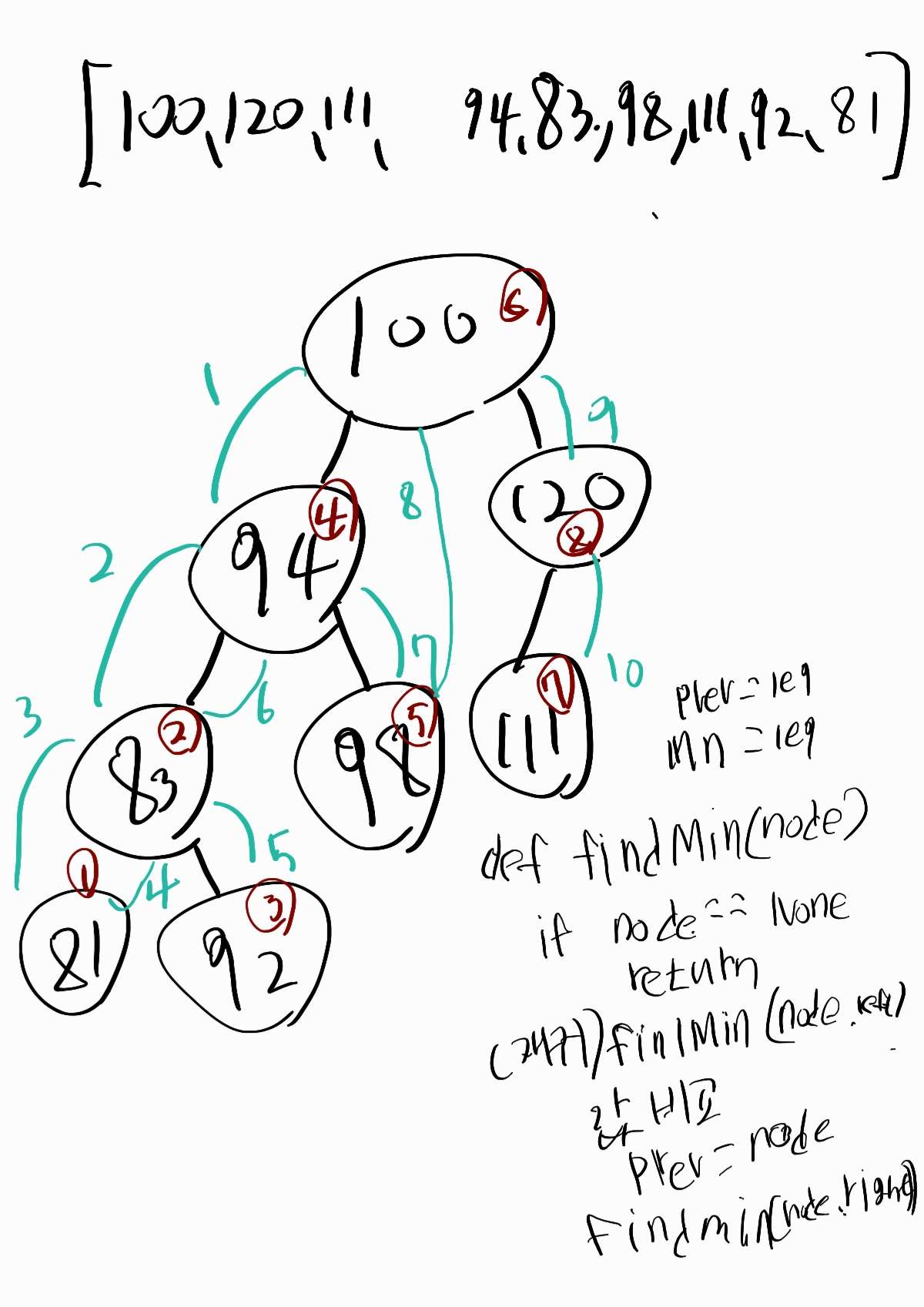
BST트리에서 오름차순으로 순화하기위해서는 중위순회를 하면 된다.
방법
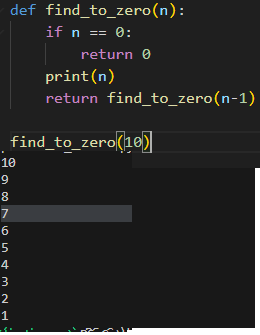
1. 중위순회를 통해서 가장 작은 값에서부터 탐색을 시작해서 탐색마다 K의 값을 1씩 빼줘서 (K = K-1) 0이되면 현재 노드의 값 반환시키기
2. 리스트를 만들어서 중위순회를 통해 값을 리스트에 담아서 리스트의 K-1번째 인덱스 반환
BST트리가 중위순회를 통해 탐색한다면 최소값부터 순회한다는걸 알면 쉬운 문제이다.
코드
1. 중위순회 반복분 (k를 차감하며 탐색)
# 재귀로 탐색
class Solution(object):
def kthSmallest(self, root, k):
self.cnt = k
self.result = None
self.find(root)
return self.result
def find(self,node): # 트리의 왼쪽아래 (DETH가 제일 깊은 왼쪽) 탐색
if node is None: # node가 None이라면 반환
return
self.find(node.left) # 왼쪽탐색 재귀 (왼쪽끝까지 간 후 탐색 시작)
self.cnt-=1 # k를 cnt로 값을 1씩 차감
if self.cnt == 0: # cnt가 0이 된다면 오름차순정렬시 k번째 인덱스의 숫자
self.result = node.val
return
self.find(node.right)2. 중위순회하며 찾은 값들을 리스트에 넣고, 리스트의 [k-1]번째 인덱스를 반환하는 방법
# 리스트로 찾기
class Solution(object):
def kthSmallest(self, root, k):
self.result = []
self.find(root)
return self.result[k-1]
def find(self,node):
if node is None: # none이라면 반환
return
self.find(node.left) # depth가 제일 깊은 왼쪽 노드로 재귀를 통해 탐색 (맨 왼쪽노드부터 탐색시작)
self.result.append(node.val) # 찾은 값 추가해주기,
self.find(node.right) # 왼쪽 현재 오른쪽 탐색,위와 동일하게 재귀문으로 왼쪽 뎁스의 가장 깊은 곳부터 탐색을 시작하며 값들을 모두 리스트에 담고
리스트[k-1]번째 인덱스의 값을 반환해준다.
다른사람의 코드
class Solution:
def kthSmallest(self, root: TreeNode, k: int) -> int:
stack = []
res = []
while stack or root:
while root:
stack.append(root)
root = root.left
root = stack.pop()
res.append(root)
root = root.right
return res[k-1].val두개의 스택을만들고 root에서 왼쪽을 wihle문으로 먼저 뽑아서 스택에 넣어준 뒤, 오른쪽 값을 찾아서 번갈아가면서 정렬해준다, - 최종적으로 오름차순정렬된 수열의 리스트가 만들어짐,
그다음 k번쨰-1 인덱스 값을 리턴하여 값을 찾는다.
'알고리즘 > LeetCode' 카테고리의 다른 글
| LeetCode 637. Average of Levels in Binary Tree (python) (0) | 2023.09.08 |
|---|---|
| 199. Binary Tree Right Side View (python) (0) | 2023.09.07 |
| LeetCode 530. Minimum Absolute Difference in BST (python) (0) | 2023.09.07 |
| LeetCode 33. Search in Rotated Sorted Array (0) | 2023.09.05 |
| 153. Find Minimum in Rotated Sorted Array (0) | 2023.09.05 |